DAG, 위상정렬(feat. BOJ. 줄세우기)
위상정렬
위상정렬(Topological Sorting)은 방향성 비순환 그래프(Directed Acyclic Graph, DAG)의 노드들을 선형으로 정렬하는 알고리즘입니다. 이 정렬은 그래프의 모든 간선이 방향성에 맞도록 순서대로 나열되도록 합니다.
DAG = 사이클이 없는 방향 있는 그래프를 의미합니다. 선행그래프 구조를 가지고 있습니다.
DAG 에서 할 수 있는 알고리즘은 위상정렬 알고리즘이 활용됩니다.
BFS 알고리즘을 응용해서 구현할 수 있습니다.
위상정렬에서 주목해서 봐야할 것은 순서와 큐 입니다.

이 상태에서 인디그리가 0인 상태인 얘들을 큐에 넣어줍니다.
큐 : 1,2,3 이 존재하고 (왜냐하면 1,2,3 노드로 들어오는 화살표가 0) 여기서 하나씩 빼면서 BFS 과정을 거쳐주게 됩니다.


순서 : 1
큐 : 2,3, 9
노드 1부터 시작하게 됩니다. 우선 노드 9로가는 간선을 지우게 되면 노드 9가 인디그리가 0이 되기 때문에 큐에 넣을 수 있습니다.
순서 : 1
큐 : 2,3,9 상태에서

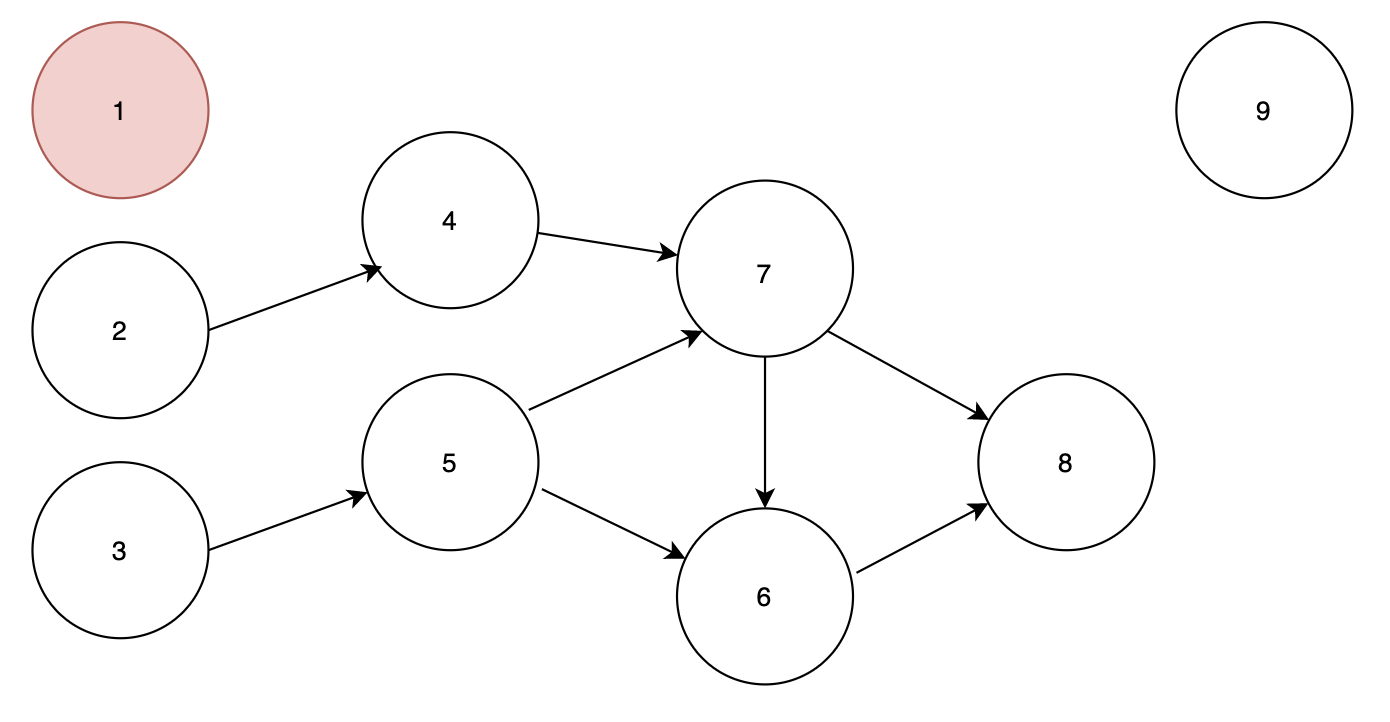
다음 노드1 에서 노드4로 가는 간선을 지우게 되더라도 노드4는 인디그리가 0이 되지 않기 때문에 큐에 포함되지 않습니다.
순서 : 1
큐 : 2,3,9
순서 : 1
큐 : 2,3,9 상태에서
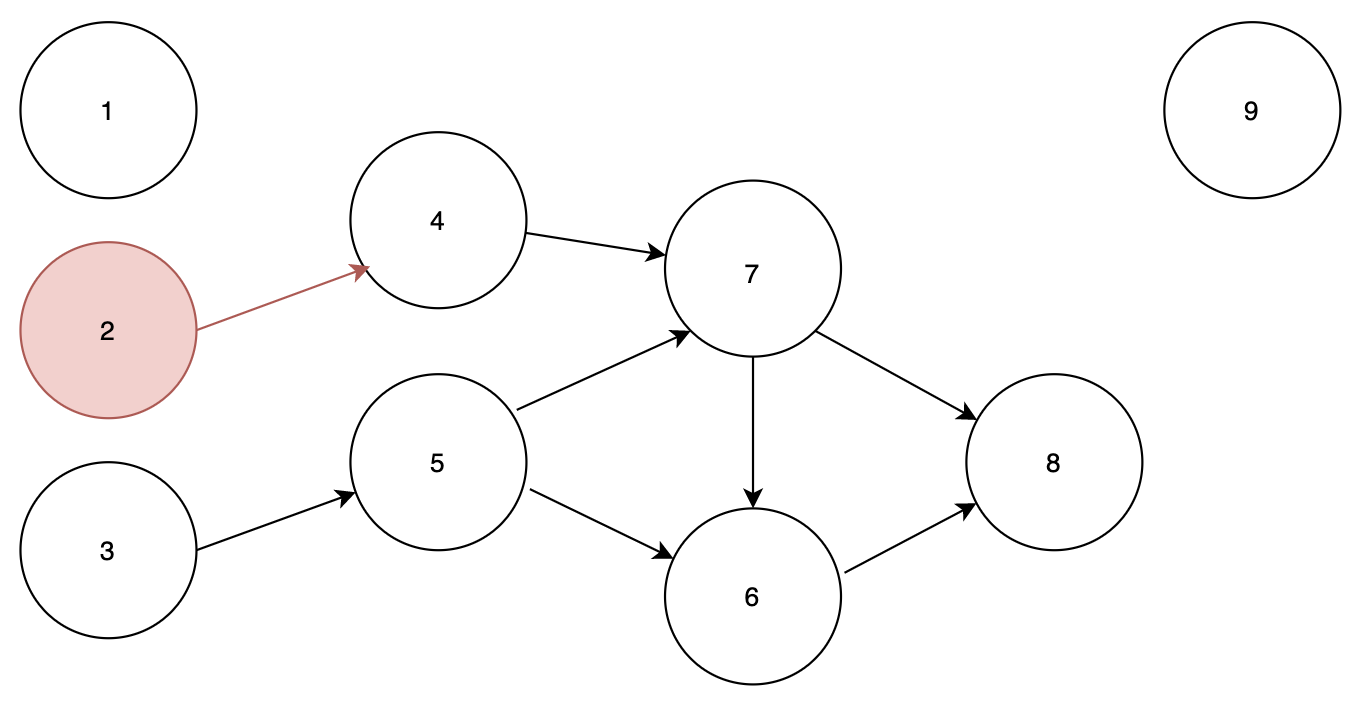
노드 2 가 시작되는 상태이므로
순서 : 1 2
큐 : 3,9
가 된다. 이때, 노드 2가 가리키고 있는 노드 4로 가는 간선을 지우게 되면
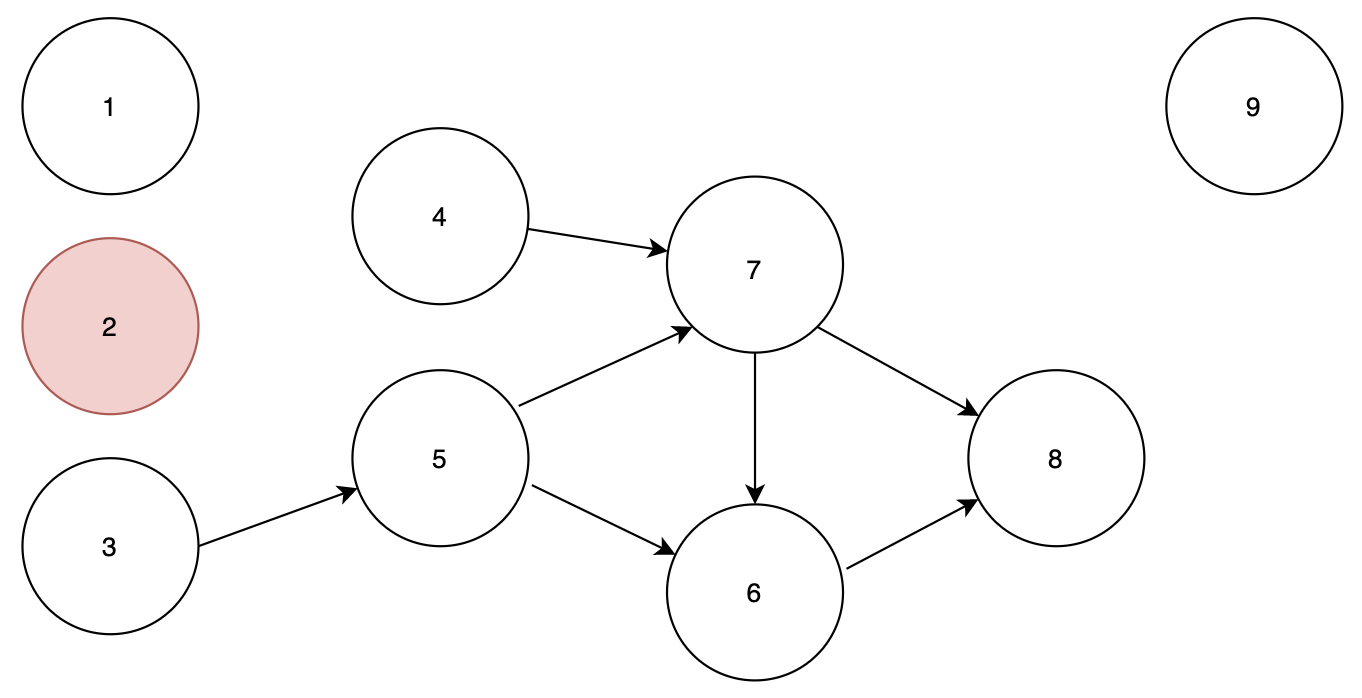
노드 4는 인디그리가 0이 되기 때문에 큐에 4가 추가 됩니다.
순서 : 1 2
큐 : 3 9 4
순서 : 1 2
큐 : 3 9 4 상태에서
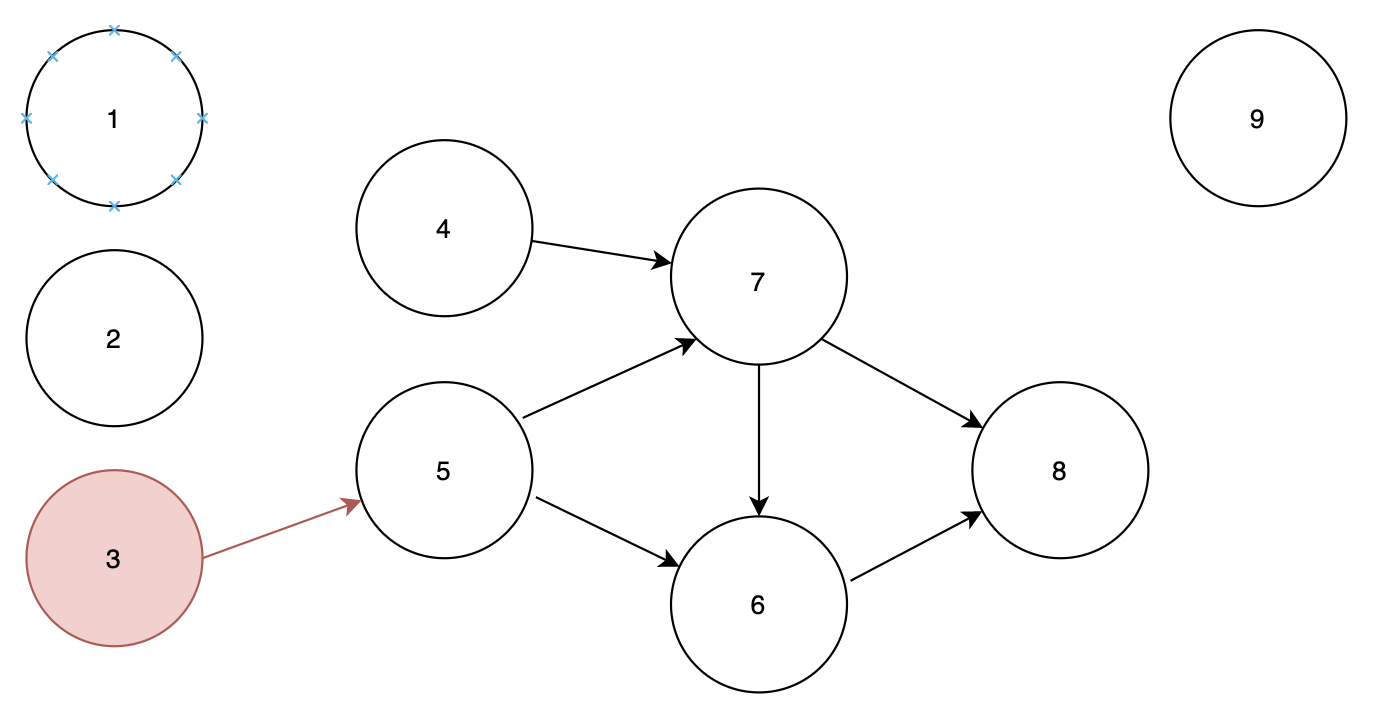
3 노드에서 시작하므로
순서 : 1 2 3
큐 : 9 4 가 됩니다.
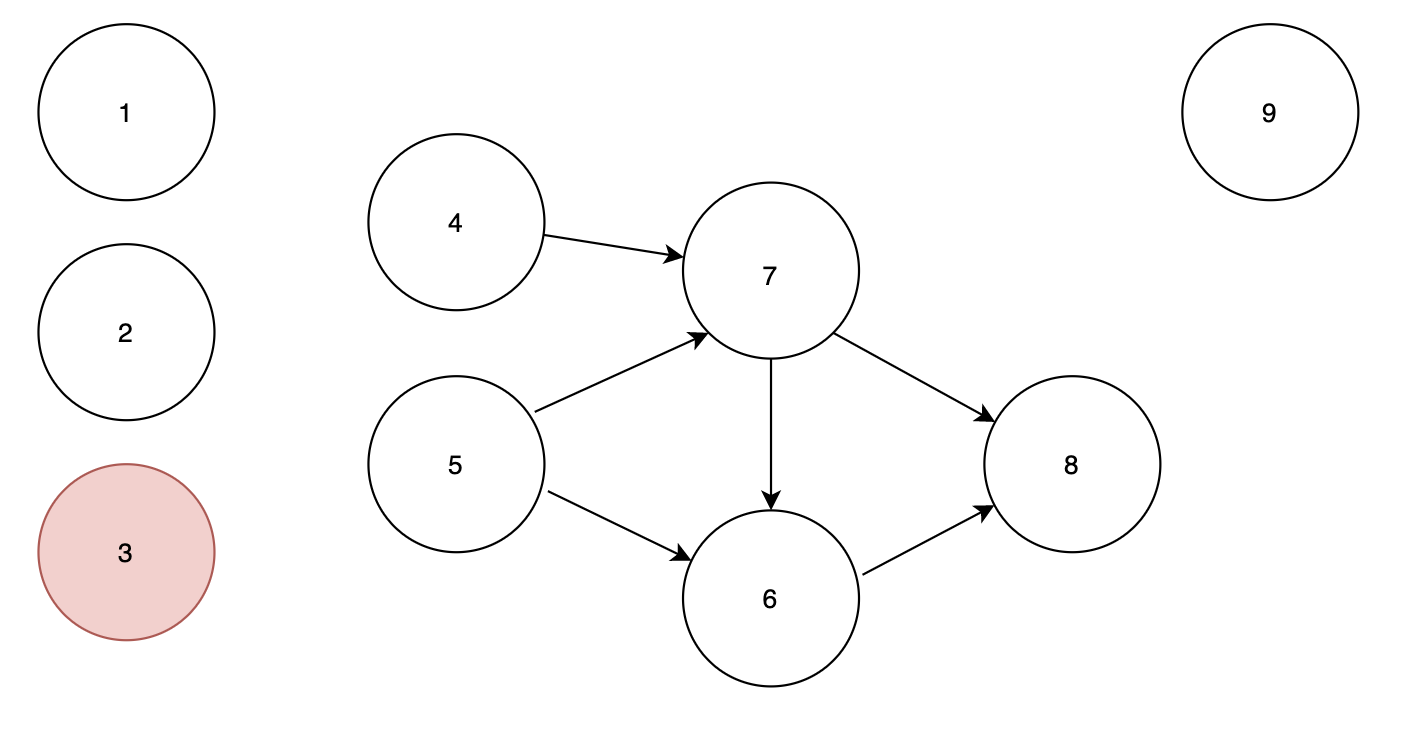
노드 3에서 노드 5로 가는 간선을 지워주면 5는 인디그리가 0이 되기 때문에
순서 : 1 2 3
큐 : 9 4 5 가 됩니다.
순서 : 1 2 3
큐 : 9 4 5 이 상태에서
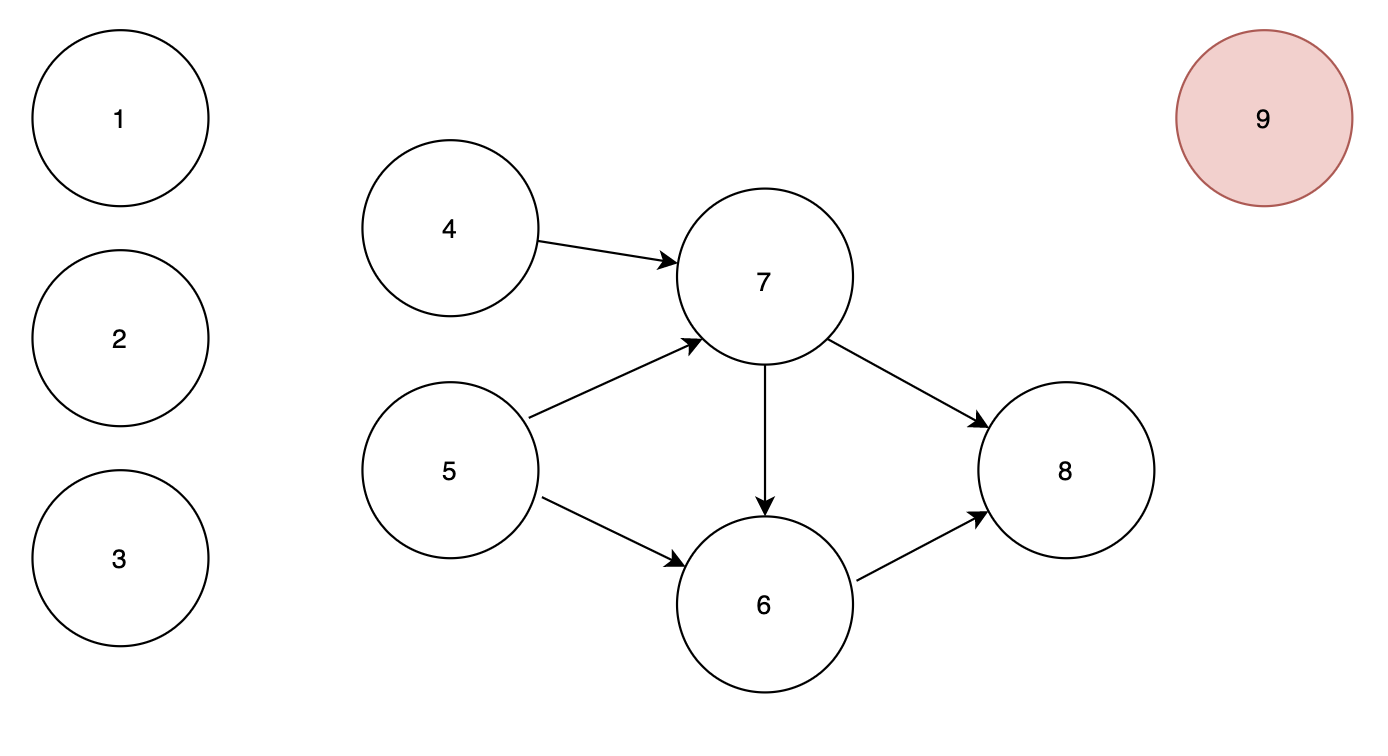
노드 9 에서 시작하면 나아갈 간선이 없습니다. 순서에 포함합니다.
순서 : 1 2 3 9
큐 : 4 5
순서 : 1 2 3 9
큐 : 4 5 상태에서 노드 4에서 시작하므로
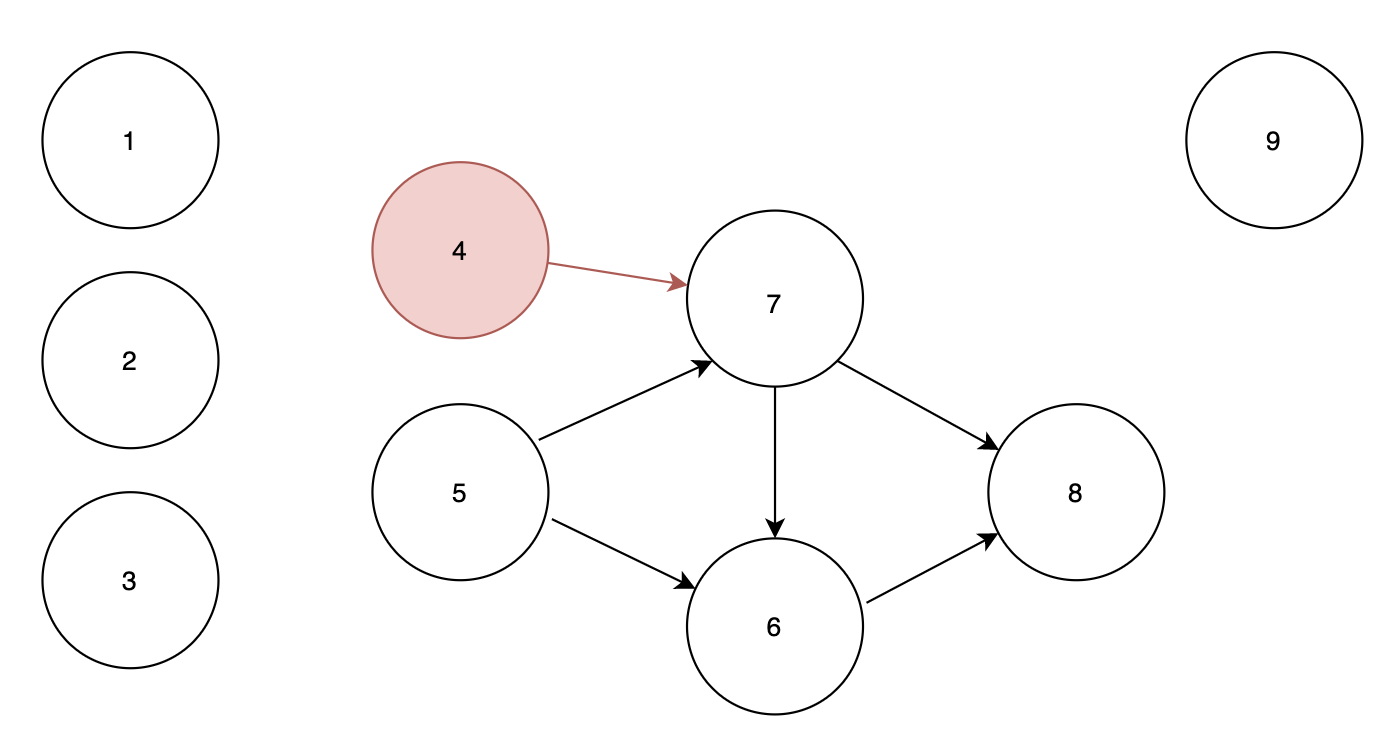
순서 : 1 2 3 9 4
큐 : 5
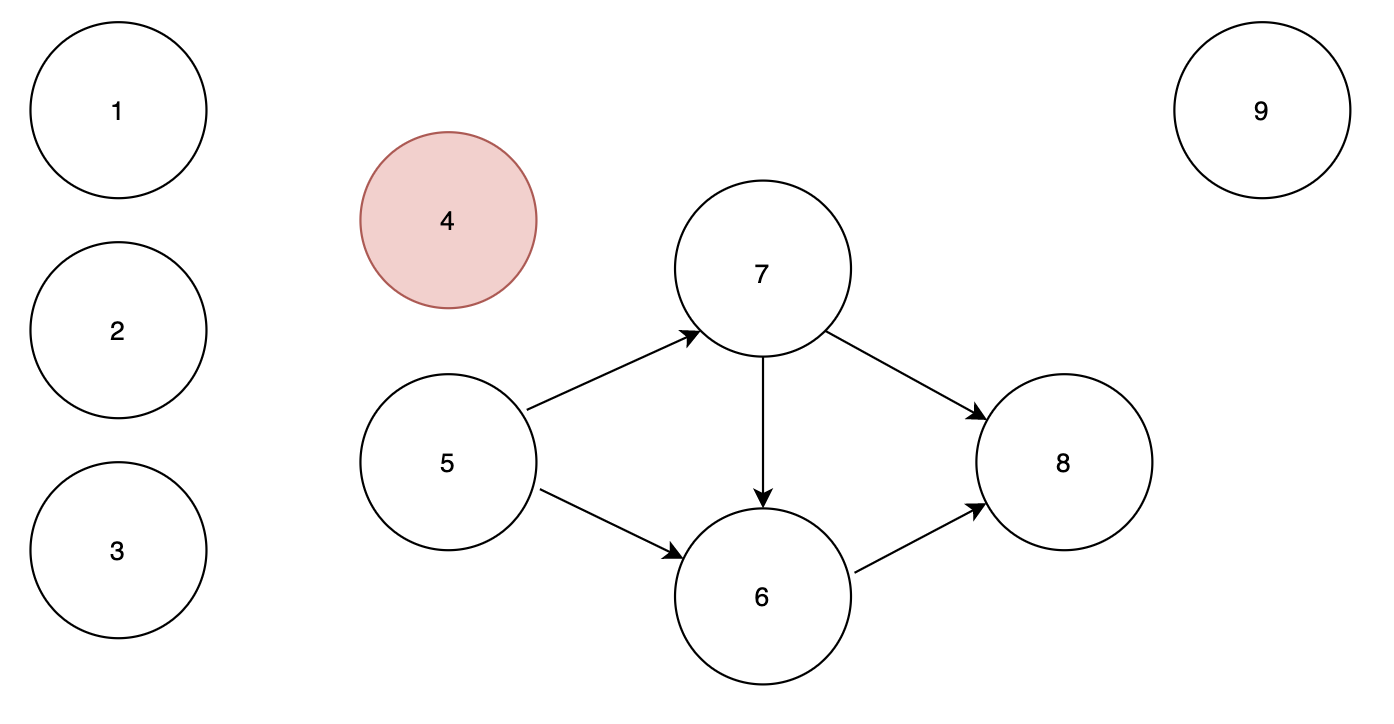
노드 4에서 노드 7로 가는 간선을 지우더라도 노드 5에서 노드 7로 가는 간선이 존재하므로 노드 7은 큐에 포함되지 않습니다.
순서 : 1 2 3 9 4
큐 : 5 상태에서 노드 5에서 시작하므로
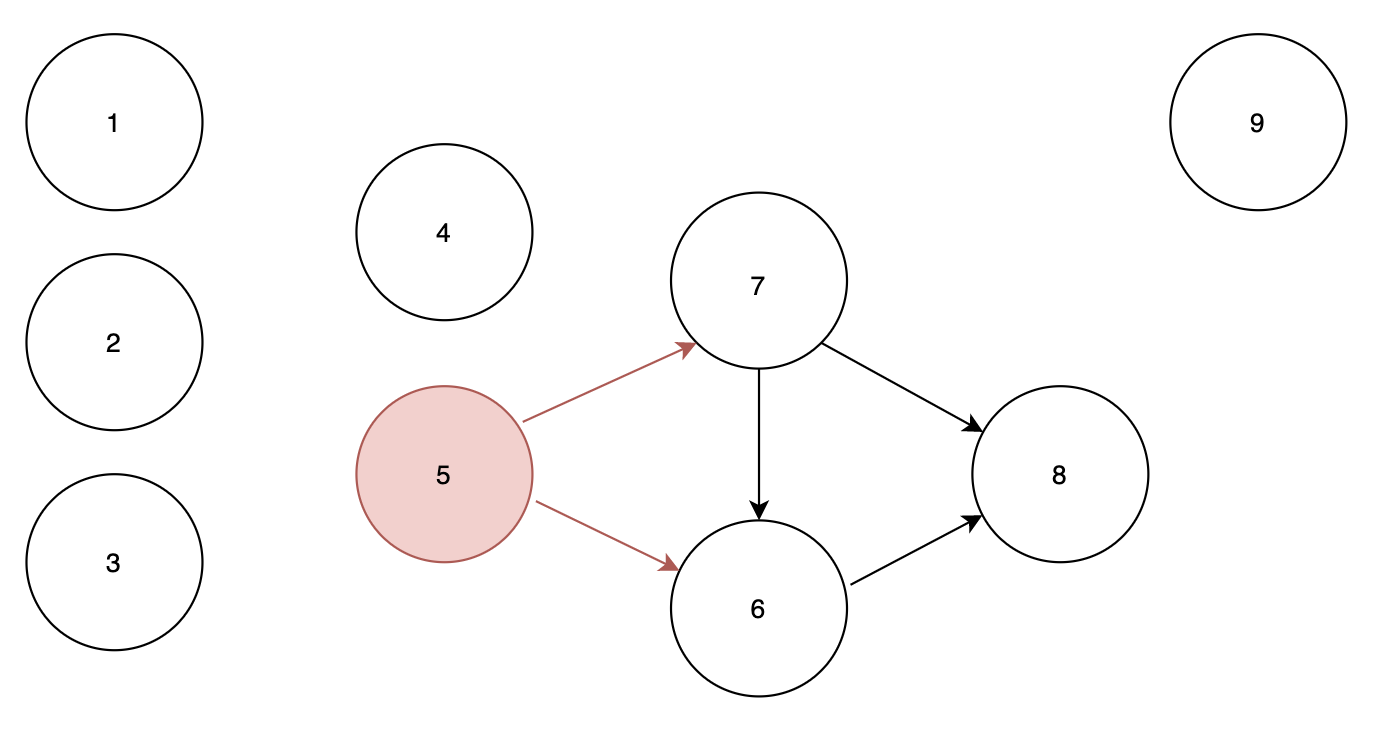
순서 : 1 2 3 9 4 5
큐 : empty
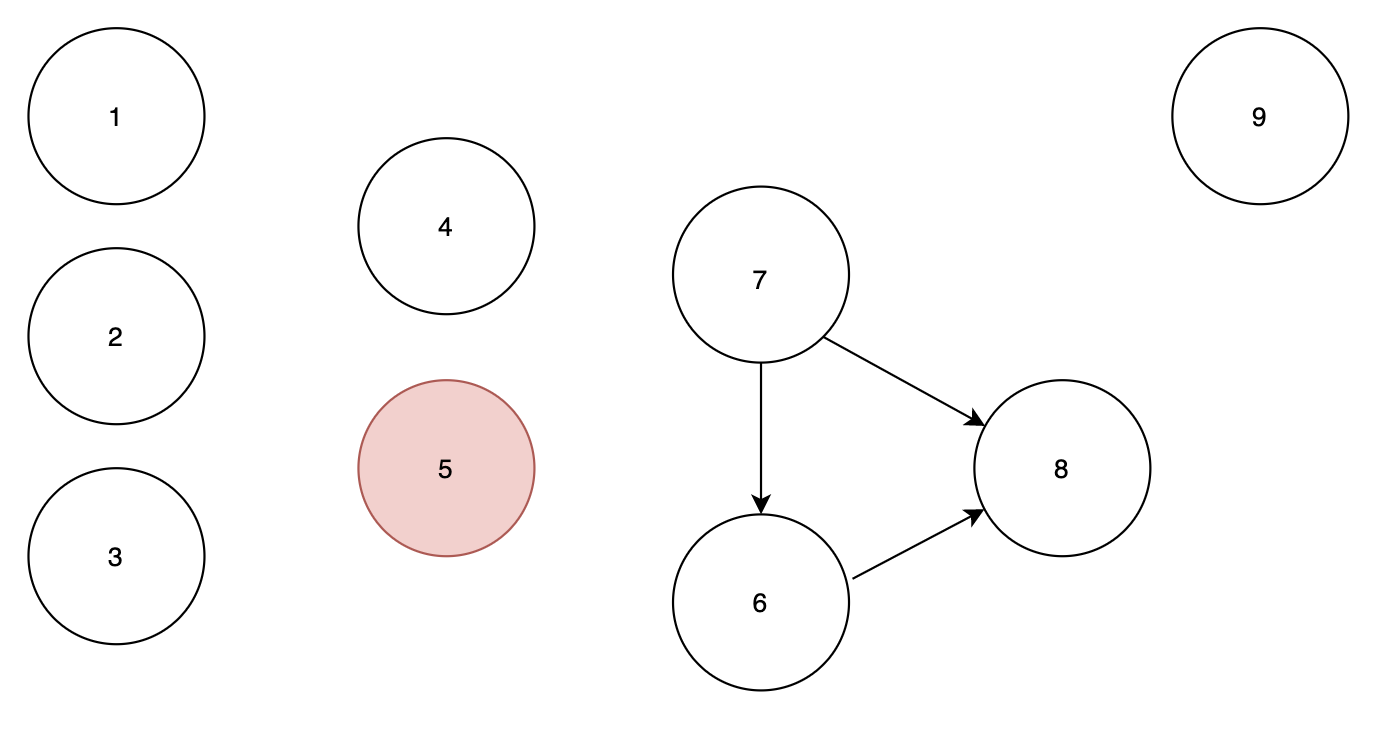
노드 5에서 노드 6, 7 로 가는 간선을 지워주게 되면
노드 7의 인디그리가 0이 되기 때문에 큐에 포함됩니다.
순서 : 1 2 3 9 4 5
큐 : 7
순서 : 1 2 3 9 4 5
큐 : 7 상태에서 노드 7에서 시작하므로
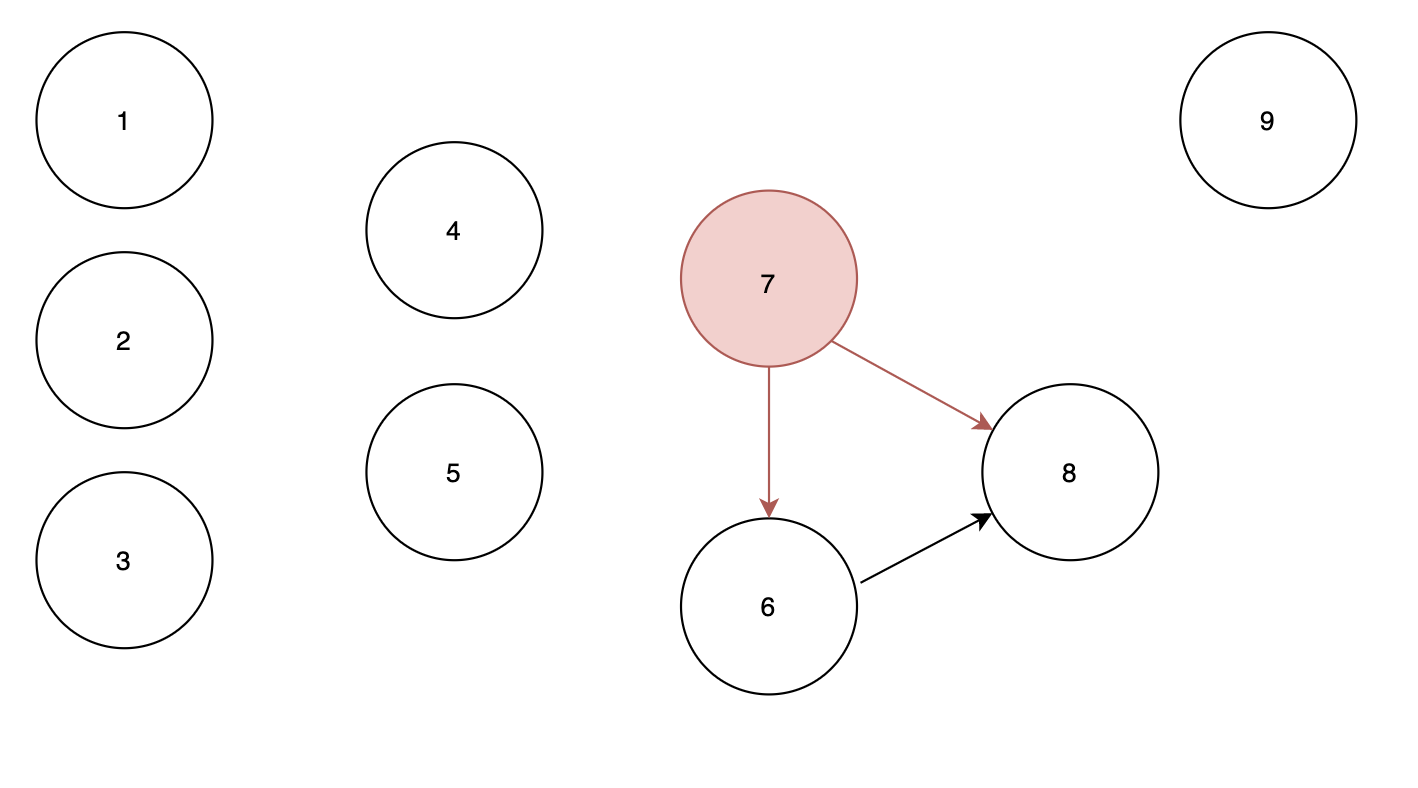
순서 : 1 2 3 9 4 5 7
큐 : empty
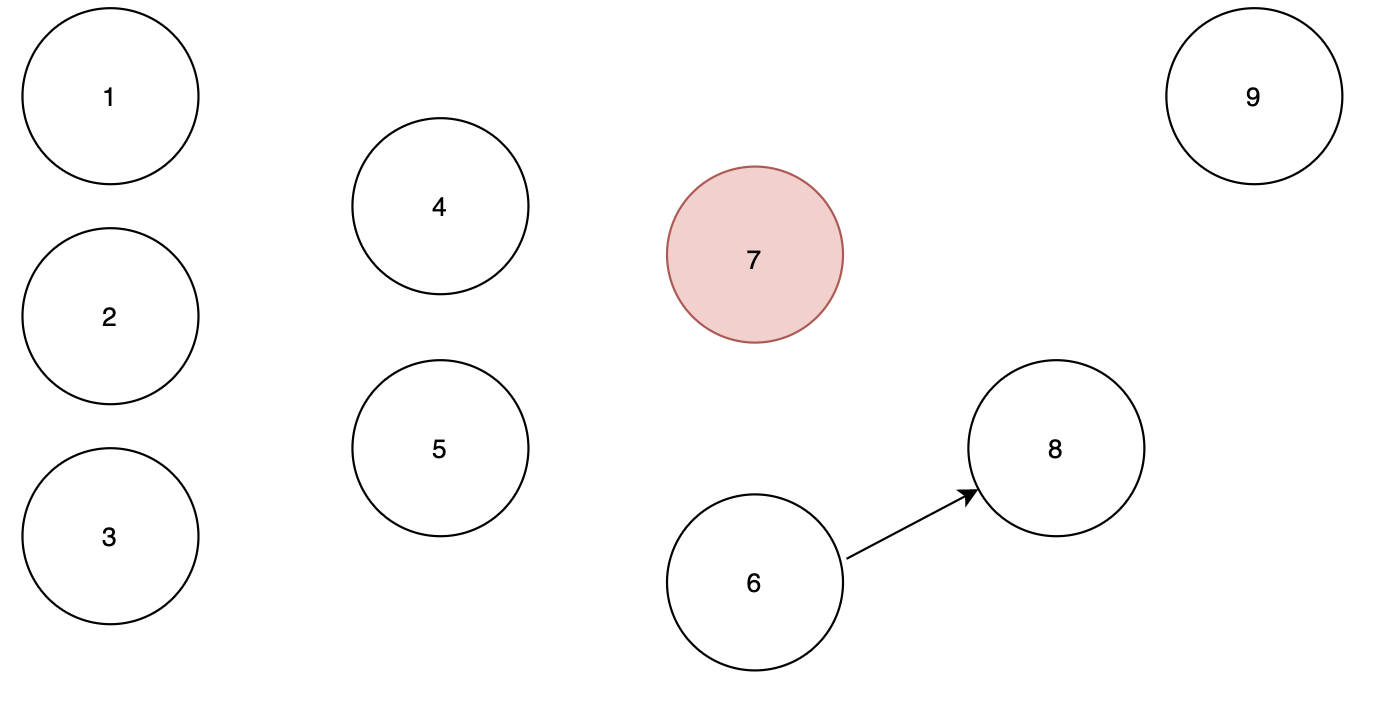
노드 7에서 노드 6, 8로 가는 간선을 제거하게 되면
노드 6이 인디그리가 0이 되기 때문에 큐에 포함됩니다.
순서 : 1 2 3 9 4 5 7
큐 : 6
순서 : 1 2 3 9 4 5 7
큐 : 6 인 상태에서 노드 6에서 시작하므로
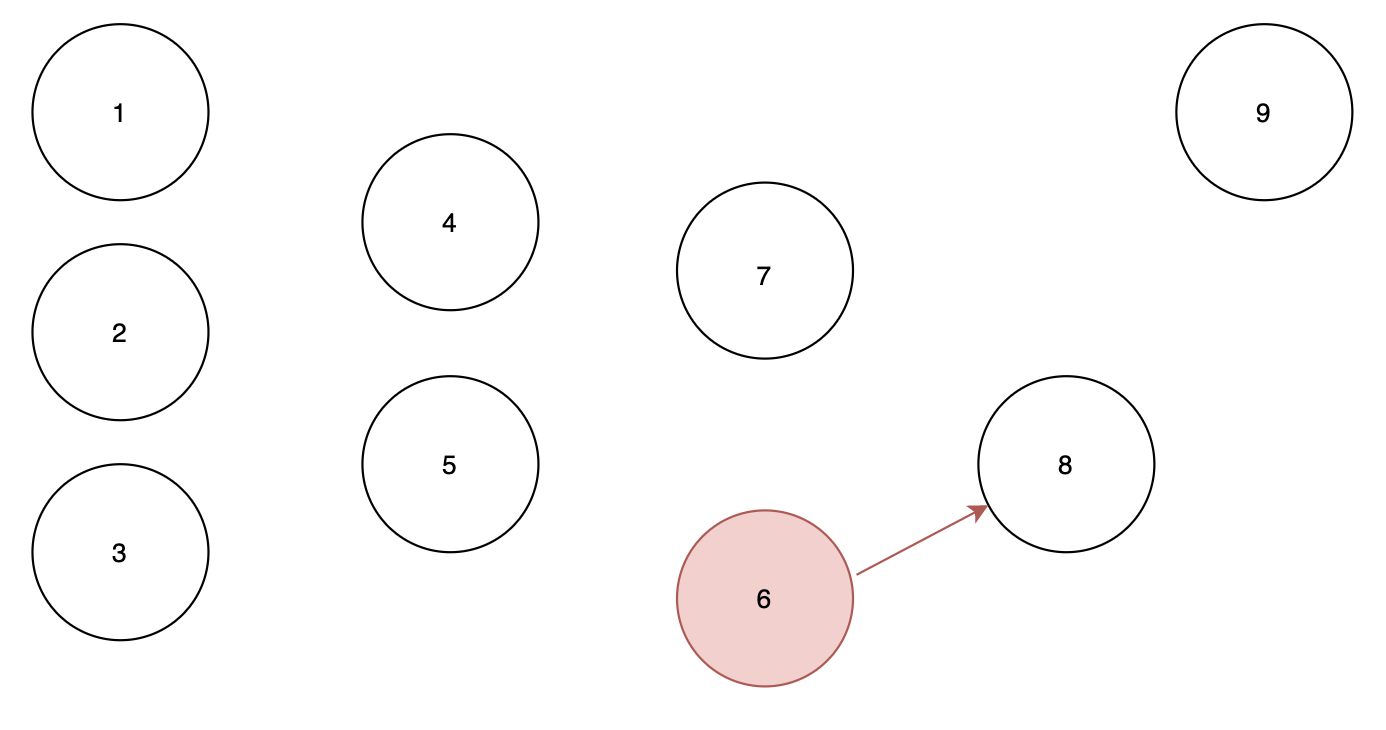
순서 : 1 2 3 9 4 5 7 6
큐 : empty
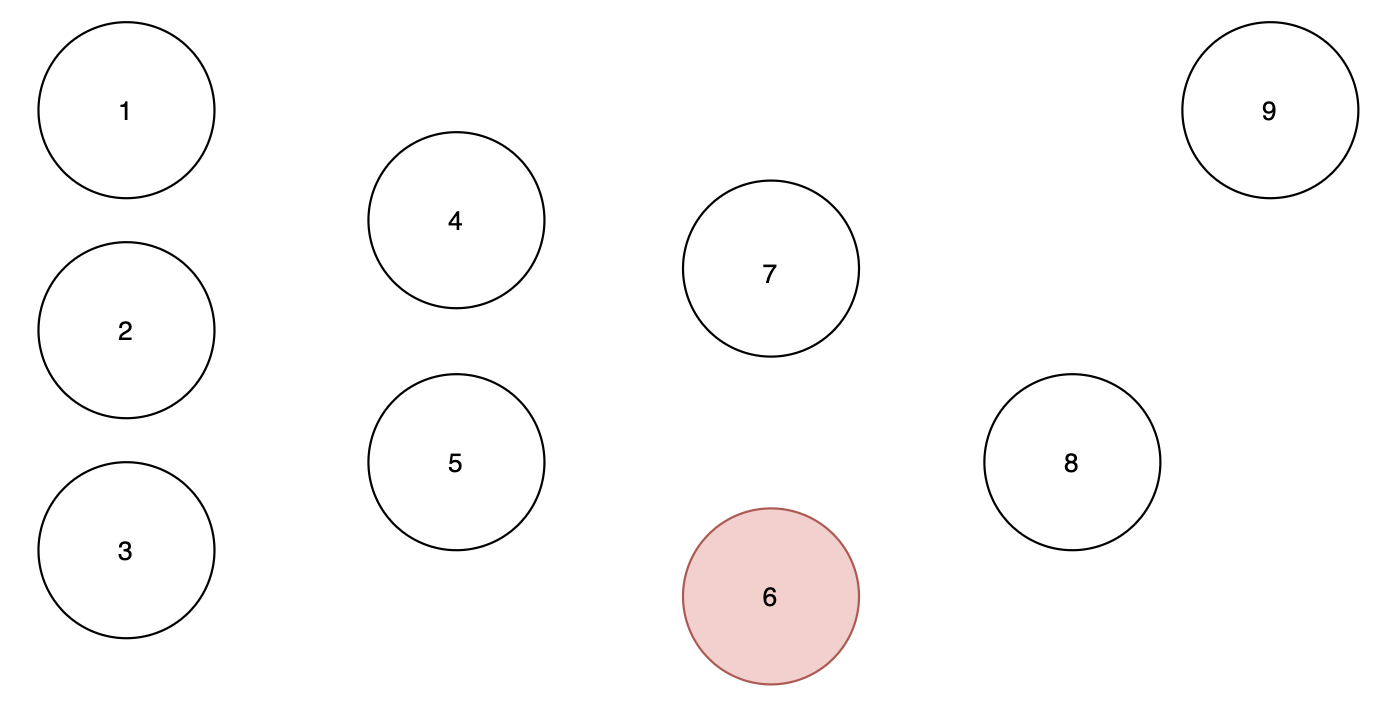
노드 6에서 노드 8로 가는 간선을 제거하게 되면
노드 8의 인디그리가 0이 되기 때문에 큐에 포함됩니다.
순서 : 1 2 3 9 4 5 7 6
큐 : 8
순서 : 1 2 3 9 4 5 7 6
큐 : 8
노드 8에서 시작하게 되므로
순서 : 1 2 3 9 4 5 7 6
큐 : empty
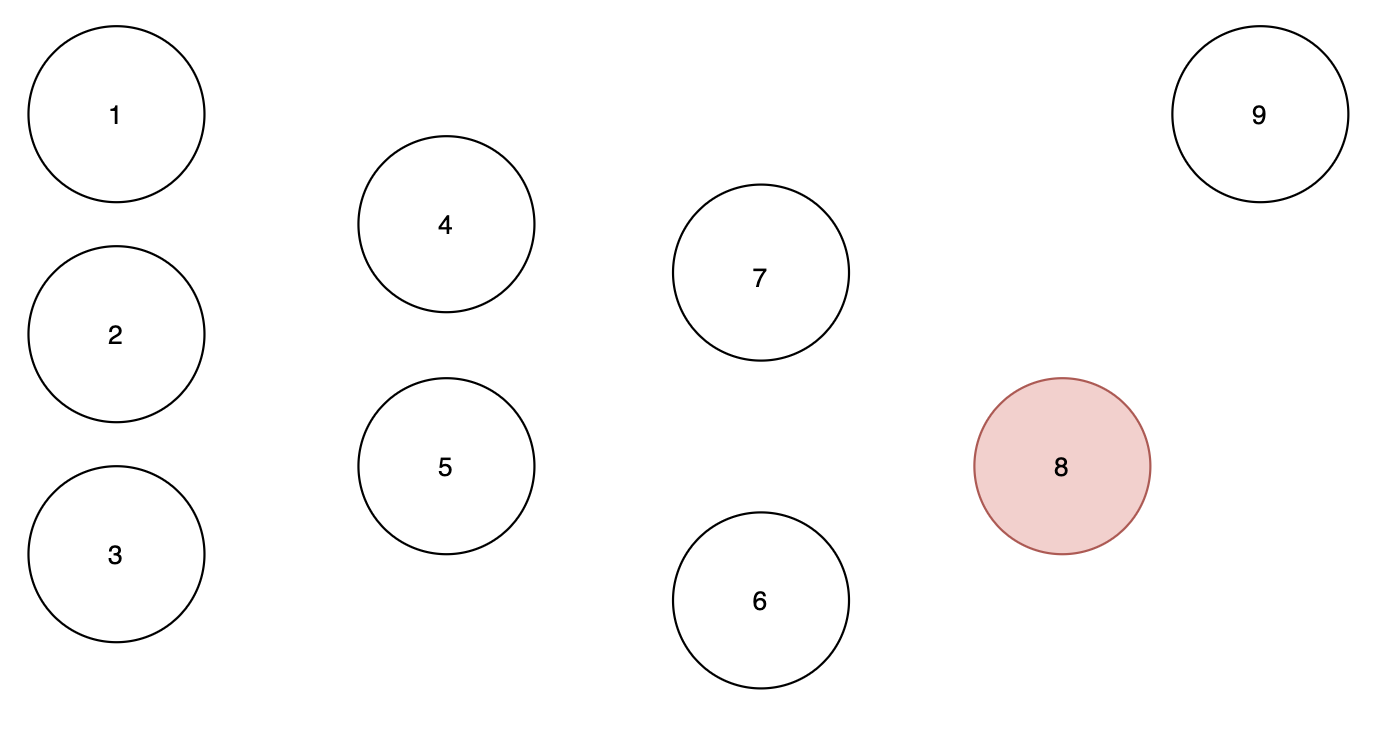
노드 8에서 아웃그리디가 존재하지 않으므로
순서 : 1 2 3 9 4 5 7 6 8
큐 : empty
종료가 됩니다.
ㅡ. 구현
백준 줄세우기 문제로 구현 연습해보겠습니다.
ArrayList<Integer> go[] = (ArrayList<Integer>[]) new ArrayList[n+1]; //어레이 리스트를 배열로 생성 for(int i=1; i<=n; i++) { go[i] = new ArrayList<>(); } //어레이 리스트를 사용하는 노드는 인접리스트를 구현하기 위함입니다.
int[] gote = new int[n+1]; for(int i=0; i<m; i++) { st = new StringTokenizer(br.readLine()); int a = Integer.parseInt(st.nextToken()); int b = Integer.parseInt(st.nextToken()); //줄세우기로 두명의 키를 입력받은후 이때 a가 b 앞에 오게 되므로 go[a].add(b); //a->b 이런 노드와 간선으로 이루어진 모습일것입니다. gote[b]++; //따라서 b 노드에 a노드 하나가 붙어있으므로 연결된 간선 하나를 증가시켜줍니다. }
Queue<Integer> q = new LinkedList<>(); for(int i=1; i<=n; i++) { if(gote[i]==0) //노드를 확인하면서 연결된 간선이 0인것(즉, 인그리디=노드로 들어오는 화살표)을 큐에 넣어줍니다. q.add(i); }
while(!q.isEmpty()) { int s = q.poll(); System.out.print(s+" "); //큐에 적재된 순서가 문제에서 요구하는 줄을 세우는 순서가 됩니다. for(int i=0; i<go[s].size(); i++) { int next= go[s].get(i); //또, 인접리스트로 구현되었기 때문에 인접된 노드를 확인 gote[next]-=1; //실제로 간선은 연결되어있지만, 간선을 삭제 한다 의미를 -1로 수행 if(gote[next]==0) //인그리디가 0이라면 큐에 적재 q.add(next); } }
⇢전체 소스코드
package backjun; import java.io.BufferedReader; import java.util.*; import java.io.*; public class backjun_줄세우기 { public static void main(String[] args) throws Exception{ // TODO Auto-generated method stub BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); int n = Integer.parseInt(st.nextToken()); int m = Integer.parseInt(st.nextToken()); ArrayList<Integer> go[] = (ArrayList<Integer>[]) new ArrayList[n+1]; for(int i=1; i<=n; i++) { go[i] = new ArrayList<>(); } int[] gote = new int[n+1]; for(int i=0; i<m; i++) { st = new StringTokenizer(br.readLine()); int a = Integer.parseInt(st.nextToken()); int b = Integer.parseInt(st.nextToken()); go[a].add(b); gote[b]++; } Queue<Integer> q = new LinkedList<>(); for(int i=1; i<=n; i++) { if(gote[i]==0) q.add(i); } while(!q.isEmpty()) { int s = q.poll(); System.out.print(s+" "); for(int i=0; i<go[s].size(); i++) { int next= go[s].get(i); gote[next]-=1; if(gote[next]==0) q.add(next); } } } }
*reference : 코드플러스
'알고리즘' 카테고리의 다른 글
| BOJ 17612 쇼핑몰 (0) | 2025.04.07 |
|---|---|
| kakao_n진수 게임 (0) | 2025.01.26 |
| 알고리즘 펜윅 트리 (2) | 2024.08.11 |
| 35. Search Insert Position (0) | 2024.06.07 |
| 979. Distribute Coins in Binary Tree (0) | 2024.05.19 |
댓글
이 글 공유하기
다른 글
-
BOJ 17612 쇼핑몰
BOJ 17612 쇼핑몰
2025.04.07 -
kakao_n진수 게임
kakao_n진수 게임
2025.01.26 -
알고리즘 펜윅 트리
알고리즘 펜윅 트리
2024.08.11 -
35. Search Insert Position
35. Search Insert Position
2024.06.07
댓글을 사용할 수 없습니다.